
こんにちは、めのんです!
前回予告したとおり、今回は境界調整について解説します。
ただ、それだけだとちょっと寂しいので、明示的な型変換についても解説することにします。
順序としては先に明示的な型変換、次で境界調整ということにしますね。
明示的な型変換
これまで暗黙の型変換についてはその都度解説してきました。
整数拡張や通常の算術型変換、既定の実引数拡張なんかもそうですね。
多くの場合は暗黙の型変換で済むのですが、一部のケースでは明示的に型変換しないといけないことがあります。
たとえばこんな場合です。
int x = 2147483647; // 32ビット符号付き整数の最大値
long long y = x * 2; // オーバーフローが発生するので未定義の動作に! 取って付けたような例ですけど、int型が32ビット符号付き整数の場合はこういうことが起こります。
xはint型ですし2もint型ですので、通常の算術型変換が行われるとしてもx * 2の評価結果もint型になります。
結果を格納するyがいくらlong long型で64ビットだったとしても、それよりも前の段階でオーバーフローが発生してしまうのです。
こういう場合は明示的な型変換が必要になります。
明示的な型変換は次のようにします。
int x = 2147483647; // 32ビット符号付き整数の最大値
long long y = (long long)x * 2; // オーバーフローしない明示的な型変換には「キャスト演算子」を使います。
PHPの公式ドキュメントにも
PHPの型キャストは、C言語と同様に動作します。
引用元: 型の相互変換
とあるように、CのキャストはPHPの型キャストと基本的には同じです。
ただし、PHPほど高度な変換はできません。
Cのキャストでできるのは、算術型どうし(整数型と浮動小数点型)の変換、ポインタ型どうしの変換、そして整数型とポインタ型の相互変換だけです。
算術型どうしの変換
算術型どうしの型変換についてはすでに「実は奥が深い算術演算」で解説しました。
明示的な型変換を行う場合でも同じルールが適用されると思ってかまいません。
整数拡張や通常の算術型変換や既定の実引数拡張が発生する文脈では、明示的な型変換を行ったとしても、変換後の型に対してさらに整数拡張や通常の算術型変換や既定の実引数拡張が発生することに注意してください。
ポインタ型どうしの変換
Cのポインタは多くの場合、ポインタどうしで相互に型変換を行うことができます。
ただしいくつかの例外があります。
- オブジェクト型や不完全型へのポインタと関数型へのポインタは相互変換できません。
- 変換後のポインタが正しく境界調整されていない場合は未定義の動作になります。
オブジェクト型や不完全型へのポインタと関数型へのポインタは相互変換できないのですが、これには理由があります。
ハーバード・アーキテクチャといって、関数が格納されるメモリ領域とオブジェクトが格納されるメモリ領域が物理的に分離されているようなコンピュータがあります。
最近でも使われているハーバード・アーキテクチャのコンピュータには、PICやAVRのようなローエンドのマイコンや一部のARMマイコン(Cortex-M3など)があります。
また主記憶では関数とオブジェクトのメモリ領域は物理的に分離されていなくても、命令キャッシュとデータキャッシュが分かれていることは普通にあります。
この場合、データキャッシュを介して関数を上書きしてからその関数を呼び出そうとしても、キャッシュが不整合を起こしているので期待通りに動作しない場合があります。
このような理由から、オブジェクト型や不完全型へのポインタと関数へのポインタは総合変換することができません。
実際にはキャストすれば変換できてしまうことが多いんですが、まともに動作しないと思った方がいいでしょうね。
境界調整に関してはこのあとすぐに解説します。
境界調整
「境界調整」という概念はすごくハードウェアよりなので、PHPなどのスクリプト言語はもちろん、Javaのような抽象度が高いプログラミング言語でもほぼ遭遇することがないと思います。
「32CPUというのはデータバスが32ビットで、64ビットCPUはデータバスが64ビットある」といった話を聞いたことがないでしょうか?
細かいことを抜きにすれば基本的にその考え方は正しいといえます。
データバスというのはCPUとメモリをつなぐ信号線のことです。
データバスが32ビットあれば32ビットの値を一度に読み書きできることを意味しています。
そして、メモリの中は32ビット単位でデータが格納されています。
32ビット単位でデータが格納されているのであれば、それより小さいサイズ、たとえば8ビットや16ビットのデータを読み書きするときは、その32ビットの中の上半分とか下半分とか下4分の1といった感じで扱います。
普通、CPUのアドレスは8ビット単位ですので、32ビットマイコンであれば32ビット単位の4分の1ごとにアドレスが振られていることになります。
次の図のように、中途半端な場所に格納された32ビット値は一度に読み書きすることができません。
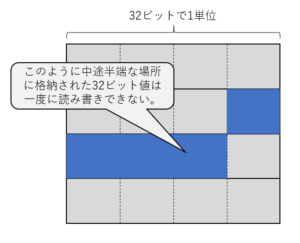
インテルのCPUは歴史的な経緯もあって中途半端な位置に格納競れているデータでも読み書きできるのですが、ハード的には2回に分割して読み書きしないといけないので効率が悪くなります。
CPUによってはそもそもこのようなアクセスを許していないものもあるので、CPU例外といってハード的なエラー処理が走ってしまったり、勝手に違うアドレスにアクセスしたりする場合があります。
こうした理由から、32ビット値であれば32ビット境界(4の倍数アドレス)に、16ビット値であれば16ビット境界(偶数アドレス)に格納する必要があります。
このことを「境界調整」と呼んでいます。
8ビットのCPUであればデータバスは8ビットですから、さきほどのような中途半端な場所というのが存在しません。
ですので、メモリ上のどこにでも任意のデータを配置することができます。
16ビットのCPUであればデータバスが16ビットですので、16ビットや32ビットなどのデータは偶数アドレスに格納すればよいことになります。
Cの話に戻ると、たとえばint型へのポインタであれば(int型が32ビットなら)32ビット境界に整列されたアドレスでなければなりません。
char型は1バイトですので、char型へのポインタであればどんなアドレスであっても境界調整に関しては問題がないことになります。
ですから、char型へのポインタからint型へのポインタに変換するよな場合は境界調整に注意しないといけないのです。
構造体の境界調整
構造体もメモリ上に格納されますから、何らかの境界調整が必要になります。
構造体にはいろんな型のメンバが混在していますが、ハード的には構造体全体を一気に読み書きすることはありません。
ですので、個々のメンバごとに境界調整ができていればそれでいいことになります。
たとえば次のような構造体を考えてみましょう。
struct A
{
char a;
int b;
};ここではint型が4バイトの32ビットCPUの処理系を仮定することにします。
メンバaは1バイトですのでどんなアドレスでもOKです。
けれどもメンバbは4の倍数アドレスでなければなりません。
このような場合は構造体全体が4の倍数アドレスに格納されなければなりません。
境界調整にもっとも大きな値を要求するメンバに構造体全体があわせることになります。
そしてメンバaのあとには3バイト分の未使用領域が発生します。
この未使用領域のことを「詰め物(padding)」といいます。
詰め物が発生することで、struct A全体のサイズは1 + 4 = 5バイトではなく1 + 3 + 4 = 8バイトになります。
3バイトは詰め物のバイト数です。
次のような構造体も考えてみましょう。
struct B
{
char a;
int b;
char c;
};メンバaとbについてはさきほどと同じです。
ところがそのあとにメンバcが追加されています。
メンバcはchar型なのでどんなアドレスにでも配置できるのですが、この場合でもメンバcのあとに3バイトの詰め物が入ります。
そうしないとstruct Bの配列を作ったときに配列のサイズがsizeof(struct B)の倍数にならないからです。
ぜひ実際に配列を作ってご自身でためしてみてくださいね。
境界調整が理解できるようになると、Cがかなり使えるようになってきたと考えていいと思います。
コンピュータの原理やハードウェアのことがわかっていないとかなり難しい話だったかもしれませんが、がんばってここは理解して欲しいと思います。
それでは今回の解説は以上になります。
次は今回やった内容を踏まえて、malloc関数やfree関数の簡単な実装例を見ていきたいと思います。
ただ、平日に書くにはちょっと重い内容なので、適当につないで次の週末まで先送りするかもしれません。
あらかじめご了承ください。






